Sábado - 20.Abril.2024 |
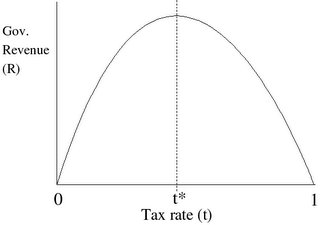
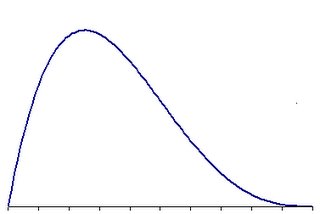
Estás en: Matemáticas Siguiendo las curvas de Laffer(14/01/2006)Autor: Ambrosio Liceaga Tengo algunos amigos que me han pedido que anime un poco más esta bitácora. Dibujos, fotografías y, sobre todo, algún tema no totalmente científico. Va a ser que no, :-). Tendrán que conformarse con algunas imágenes para hacer menos árido un tema bastante diferente. Hablaremos de la que dicen que fue la segunda profesión más antigua. La recaudación de impuestos. Autor: Ambrosio Liceaga Visitas: 5772 Comentariosinvitado el 14/06/2010: Que exista una curva es una cosa, pero lo interesante es saber que curva. Decir que es la curva de Laffer es un acto de fé. Imagina que fuese una curva similar a la de f(x)=sin(1/x) tendriamos infinitos maximos y minimos. Bucan el 01/10/2009: Pienso que la curva de Laffer, es cierta. Otra cosa es averiguar el tipo exacto de curva que se ajusta a cada país, que variará en función de su estructura económica. Pero que la presión fiscal en España ha pasado del punto máximo se refleja en la economía sumergida, que es del orden del 20% del PIB, unos 240.000 millones anuales, de los que se dejan de ingresar, 80.000 millones de euros. Cuando la economía sumergida en un país pasa del 10%, más o menos, es que ha sobrepasado el punto máximo de la curva de Laffer e insistir en cobrar más impuestos, sólo generará más economía sumergida, pero no más recaudación, amén de atentar contra la producción de riqueza y el crecimiento económico. amx el 16/04/2008: Para divertirse un poco sobre el tema, hay un artículo de Martin Gardner en la revista Investigación y Ciencia núm. 65 de FEBRERO de 1982. Seguramente también está en alguna de la muchas recopilaciones del autor, que no conozco. La forma de la curva real, sugiere, tiene pinta de estropajo (o garabato de niño) con dos hilillos que van del (0,0) al (1,0) |
 Licencia: Licencia:
|
Uso de cookies
Utilizamos cookies propias y de terceros para mejorar la experiencia de navegación y ofrecer contenidos y publicidad de interés. Al continuar con la navegación entendemos que se acepta nuestrapolítica de cookies. Aceptar